Table of Contents
1. Systems of Linear Equations
1.1 Systems of linear equations
1.2 Matrices and linear systems
1.3 Elementary row operations
1.4 Echelon forms of a matrix
1.5 Solution set of a system of linear equations
1.6 Gaussian elimination
1.7 Gauss-Jordan elimination
1.8 Applications: Matrices in chemistry
1.9 Application: Electric circuits
2. Matrix Algebra
2.1 Matrix addition and scalar multiplication
2.2 Matrix multiplication
2.3 Matrix equations and linear systems
2.4 Inverse of a matrix
2.5 Solving a system using an inverse matrix
2.6 Elementary matrices
2.7 Block matrices
2.8 LU decomposition
2.9 Application: Leontief models
2.10 Application: Markov chains
3. Introduction to Vectors
3.1 Introduction to vectors
3.2 Vector operations
3.3 Dot product
3.4 Cross product
3.5 Application: 3D coordinate geometry
3.6 Application: Vectors in physics
4. Euclidean Vector Spaces
4.1 Vector spaces and subspaces
4.2 Spanning sets
4.3 Linear independence and dependence
4.4 Basis and dimension
5. Determinants
5.1 Introduction to determinants
5.2 Cofactor expansions
5.3 Application: Area and volume
5.4 Properties of determinants
5.5 Invertibility and determinants
5.6 Cramer’s rule
5.7 Permutations and determinants
6. General Vector Spaces
6.1 General vector spaces
6.2 Subspaces
6.3 Coordinatization
6.4 Four fundamental subspaces
6.5 Rank and nullity
7. Linear Transformations
7.1 Linear transformations between Euclidean spaces
7.2 General linear transformations
7.3 Isomorphisms
7.4 Rank and nullity of a linear transformation
7.5 Composition of linear transformations
7.6 Fundamental Theorem of Matrix Representations
7.7 Application: Transformations in 2D coordinate geometry
8. Eigenvalues and Eigenvectors
8.1 Eigenvalues and eigenvectors
8.2 Eigenspaces
8.3 Similarity and diagonalization
8.4 Complex eigenvalues and eigenvectors
8.5 Application: Inertia tensors
8.6 Application: Systems of first order differential equations
9. Inner Product Spaces and Orthogonality
9.1 Inner product spaces
9.2 Norms and distances
9.3 Orthogonal bases
9.4 Orthogonal complements
9.5 Orthogonal matrices
9.6 Singular value decomposition
9.7 Pseudoinverses
9.8 Complex inner product spaces
9.9 Application: Least-squares approximation
9.10 Application: Principal component analysis
10. Appendix: Notation
10.1 Notation
A new and interactive introduction to linear algebra and matrix theory
Linear Algebra uses an interactive approach to build comprehension of this subject’s foundational ideas. Definition-based topics are introduced to connect new concepts as the book progresses. This book includes:
- New block proof tool that helps students learn how formal math proofs are written
- 350+ auto-graded participation activities intended as reading exercises, such as question sets and animations
- 300+ end-of-section exercises for practice or homework
- Homework-appropriate, auto-graded, and randomized challenge activities in every section
- Dozens of applications connect key concepts in linear algebra to real-world examples in physics, chemistry, circuits, and more
- Adopters have access to a test bank with over 200 questions
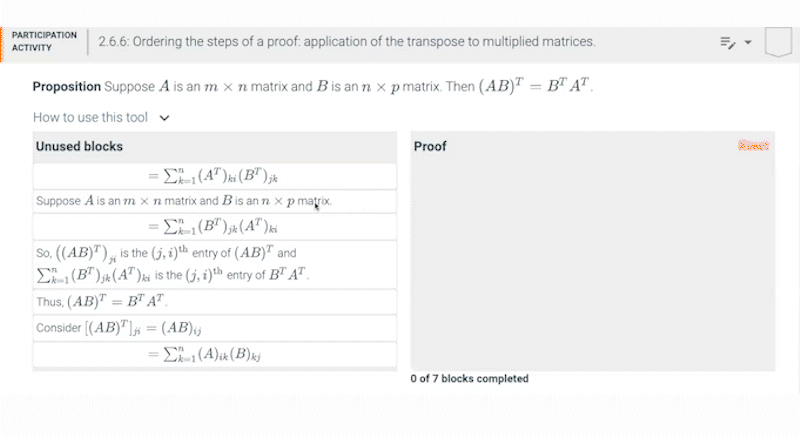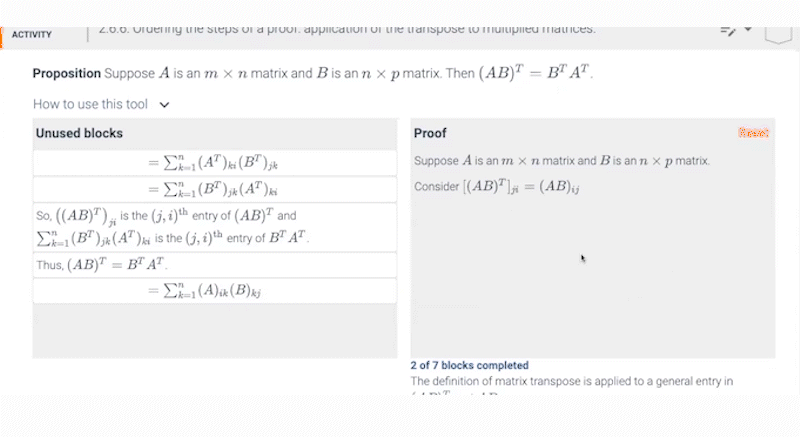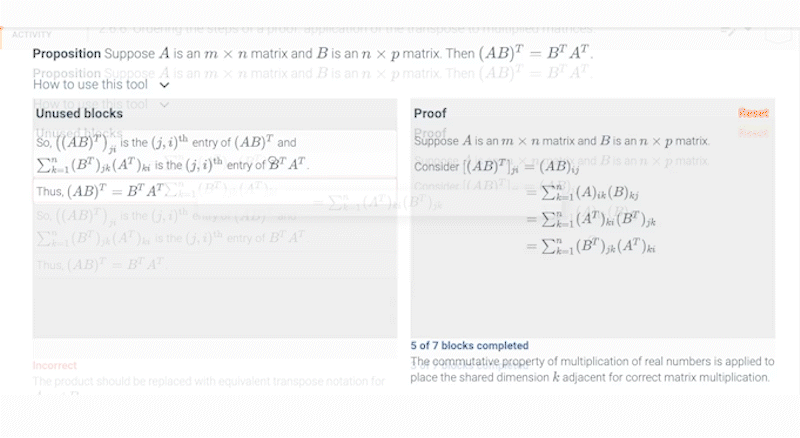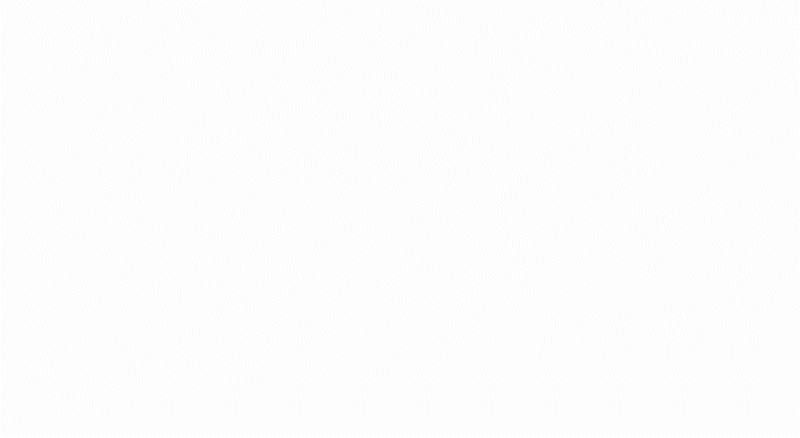
Example of proof from Linear Algebra:
What is a zyBook?
Linear Algebra is a web-native, interactive zyBook that helps students visualize concepts to learn faster and more effectively than with a traditional textbook. (Check out our research.)
Since 2012, over 1,800 academic institutions have adopted digital zyBooks to transform their STEM education.
zyBooks benefit both students and instructors:
- Instructor benefits
- Customize your course by reorganizing existing content, or adding your own content
- Continuous publication model updates your course with the latest content and technologies
- Robust reporting gives you insight into students’ progress, reading and participation
- Save time with auto-graded labs and challenge activities that seamlessly integrate with your LMS gradebook
- Build quizzes and exams with hundreds of included test questions
- Student benefits
- Learning questions and other content serve as an interactive form of reading
- Instant feedback on labs and homework
- Concepts come to life through extensive animations embedded into the interactive content
- Review learning content before exams with different questions and challenge activities
- Save chapters as PDFs to reference the material at any time
Authors
Alan Bass
Senior Content Developer, Mathematics / MS in Mathematics, University of North Carolina, Wilmington
Susan Lauer
Content Developer, Mathematics / PhD in Mathematics, Auburn University
Chris Chan
MA in Mathematics, San Francisco State University